Similar Triangles Lesson
Definition of Similar Triangles
Two triangles are considered similar if they have the same shape. To have the same shape, they must have the same angles and their sides must be in proportion. They do not have to be the same size.
In other words, similar triangles are scaled copies of each other. One could be scaled up by a factor of 2 from the other, scaled down by a factor of 0.35, etc.
Similar is not the same as congruent. To be congruent, triangles must have the same shape AND the same size.
INTRODUCING

Similar Triangles Example Problem
To reinforce our understanding of similar triangles, let's work through an example together. We will use the triangles in the image below for this example.
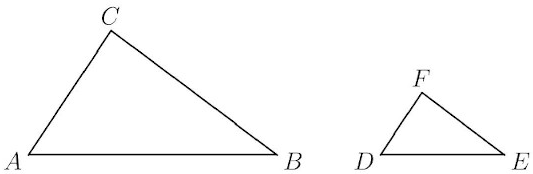
- Triangle ABC and DEF are similar.
- Side AB = 10
- Side BC = 8
- Side CA = 6
- Side DE = 5
What are the lengths of sides EF and FD?
Solution:
- The triangles are similar but not the same size. Let's determine the scaling factor between the two, then we can multiply that by the side lengths of triangle ABC.
- The ratio between the bottom sides is: DE⁄AB = 5⁄10 = 1⁄2 = 0.5
- Therefore, triangle DEF is scaled down from triangle ABC by a factor of 0.5.
- To find side EF, we will scale side BC. EF = 0.5BC = 0.5(8) = 4
- To find side FD, we will scale side CA. FD = 0.5CA = 0.5(6) = 3
- The length of side EF is 4 and the length of side FD is 3.

