What is the Side Splitter Theorem?

The side splitter theorem applies to all triangles. It tells us that:

If a line is parallel to one side of a triangle and intersects the other two sides, it divides those two sides into proportional segments.

Side Splitter Theorem Example Problem

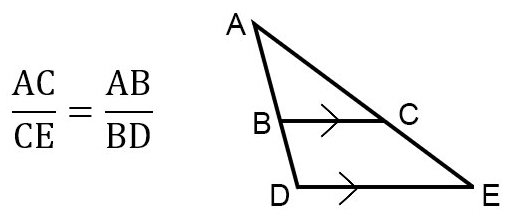
Triangle ADE in the image above is intersected by line BC. Line BC is parallel to side DE. If side AE is 7 long, segment AC is 5 long, and segment AB is 3 long, what is the length of segment BD?

Solution:

1. The side splitter theorem tells us that ^AC⁄_CE = ^AB⁄_BD.
2. We need the length of segment CE before we can solve for BD.
   AC + CE = AE
   5 + CE = 7
   CE = 2
3. Now, let's evaluate the ratio ^AC⁄_CE.
   ^AC⁄_CE = ⁵⁄₂
4. We can now apply the side splitter theorem to find the length of BD.
   ^AC⁄_CE = ^AB⁄_BD
   ⁵⁄₂ = ³⁄_BD
   BD = ⁶⁄₅
5. Segment BD is ⁶⁄₅ long.