Menu
Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Properties of a Parallelogram
Lesson Contents
The Six Main Properties of a Parallelogram
A parallelogram is a quadrilateral with two pairs of parallel sides. The six main properties of a parallelogram are given as:
1.) Opposite sides are parallel.
2.) Opposite sides are congruent.
3.) Opposite angles are congruent.
4.) The diagonals bisect each other.
5.) Adjacent angles are supplementary (meaning their sum is 180°).
6.) If one angle is 90°, then all angles are 90°.
Examples of the Properties Being Applied
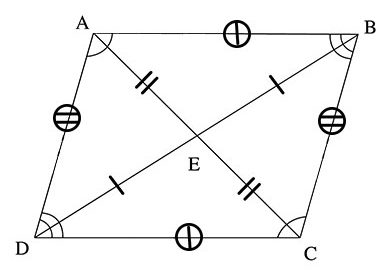
Let’s go through an example where we apply the 6 properties to parallelogram ABCD above.
1.) Opposite sides are parallel.
Side AB is parallel to side DC.
Side AD is parallel to side BC.
2.) Opposite sides are congruent.
Side AB is equal in length to side DC.
Side AD is equal in length to side BC.
3.) Opposite angles are congruent.
∠A = ∠C
∠B = ∠D
4.) The diagonals bisect each other.
Diagonal AC passes through the center of diagonal BD.
Diagonal BD passes through the center of diagonal AC.
5.) Adjacent angles are supplementary (meaning their sum is 180°).
∠A + ∠B = 180°
∠B + ∠C = 180°
∠C + ∠D = 180°
∠D + ∠A = 180°
6.) If one angle is 90°, then all angles are 90°.
If ∠A = 90°, then ∠B, ∠C, and ∠D are also 90°.
