Perimeter of a Triangle Lesson
The Perimeter Formula
A triangle is a polygon with three sides and three vertices. The formula for perimeter is given as:
P = a + b + c
Where P is the perimeter, and a, b, and c are the three side lengths.
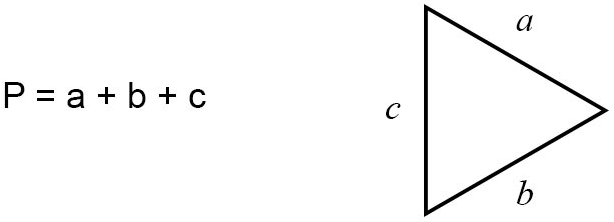
INTRODUCING

Perimeter of a Triangle Example Problems
Let's go through a couple of example problems to practice finding the perimeter of a triangle.
Example Problem 1
What is the perimeter of a triangle with side lengths of 5, 6, and 3?
Solution:
- Let’s plug the side lengths into the perimeter formula.
- P = a + b + c
- P = 5 + 6 + 3 = 14
- The perimeter of the triangle is 14.
Example Problem 2
An equilateral triangle has a perimeter measured to be 81 centimeters. What are the side lengths?
Solution:
- Since an equilateral triangle has three equal sides, a = b = c. We can substitute a + b + c with 3a.
- Plugging what we know into the perimeter formula, we get:
P = a + b + c
81 = 3a
a = 27, b = 27, c = 27 - The three sides each have a length of 27 centimeters.

