Perimeter of a Trapezoid Lesson
The Perimeter Formula
A trapezoid is a quadrilateral with only one pair of parallel sides.
The formula for perimeter is given as:
P = a + b + c + d
Where P is the perimeter, a and b are the base lengths, and c and d are the leg (side) lengths.
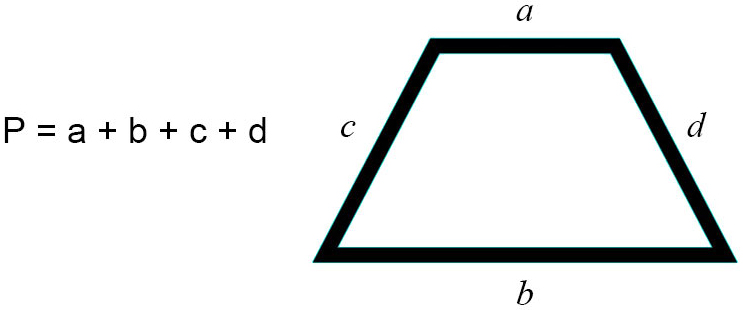
INTRODUCING

Perimeter of a Trapezoid Example Problems
Let's go through a couple of example problems to reinforce our understanding of the perimeter of a trapezoid.
Example Problem 1
Find the perimeter of a trapezoid with leg lengths of 10 and 12, and base lengths of 6 and 8.
Solution:
- All we need to do is add the 4 sides together, just as the formula says:
P = a + b + c + d - P = 6 + 8 + 10 + 12 = 36
- The perimeter of the trapezoid is 36.
Example Problem 2
A trapezoidal floor plan's perimeter is measured to be 12 meters. The bases are measured as 3 and 4 meters, and the leg sides (labeled c and d in the image above) are equal in length. What is the length of the legs?
Solution:
- Since the legs are equal in length, c = d. We can replace c + d in the perimeter formula with 2c.
- Plugging what we know into the formula, we get:
P = a + b + c + d
12 = 3 + 4 + 2c
5 = 2c
c = 2.5, d = 2.5 - The length of each leg side is 2.5 meters.

