The Perimeter Formula

The formula for perimeter of a semicircle is given as:

P = r(π + 2)

Where P is the perimeter and r is the radius.

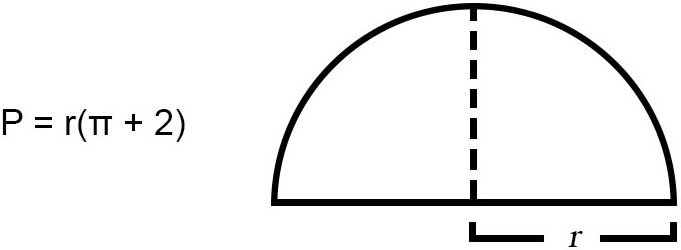
Where the Semicircle Formula Comes From

The formula is created by halving the circle perimeter formula (circumference) and adding the diameter length to that.

Perimeter of a full circle is P = 2πr, so half of that is πr, which gives us the top arc's length for the semicircle. The bottom side of the semicircle is equal to the circle's diameter, so it is 2r since d = 2r.

Adding the two components, we get P = πr + 2r. We factor out the r from both terms and get P = r(π + 2) as the final formula.

Perimeter of a Semicircle Example Problems

Let's go through a couple of example problems together to practice finding the perimeter of a semicircle.

Example Problem 1

Find the perimeter of a semicircle with a diameter of 10.

Solution:

1. First, we need to find the radius.
   r = ^d⁄₂ = ¹⁰⁄₂ = 5
2. Now we will plug the radius into the formula.
   P = r(π + 2)
   P = 5(π + 2) = 25.708
3. The perimeter is 25.708.

Example Problem 2

Find the perimeter of a semicircle with a radius of 8.

Solution:

1. Plugging the radius directly into the formula, we get:
   P = r(π + 2) = 8(π + 2) = 41.133
2. The perimeter is 41.133.

Example Problem 3

A semicircle has a perimeter of 27. What is the radius?

Solution:

1. Let's plug the perimeter into the formula and solve for radius.
   P = r(π + 2)
   27 = r(π + 2)
   ²⁷⁄_{(π + 2)} = r
   r = 5.251
2. The radius is 5.251.