The Perimeter Formula

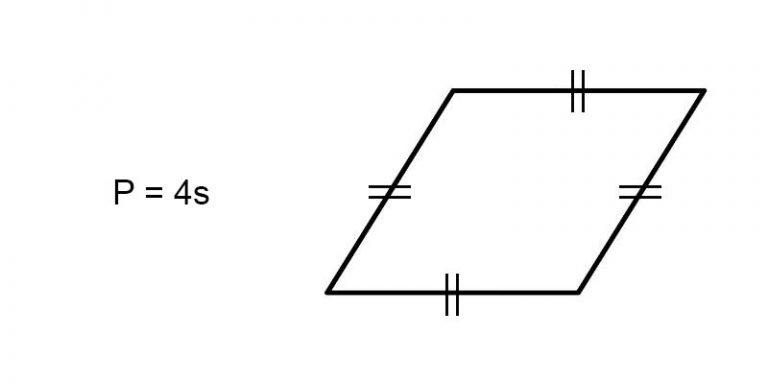
A rhombus is a quadrilateral with 4 equal sides, a pair of opposing equal acute angles, and a pair of opposing equal obtuse angles.
The formula for perimeter of a rhombus is given as:
P = 4s
Where P is the perimeter and s is the side length.

Perimeter of a Rhombus Example Problems

Let's go through a couple of example problems together to practice finding the perimeter of a rhombus.

Example Problem 1

Find the perimeter of a rhombus with a side length of 10.

Solution:

1. Since we are given the side length, we can plug it straight into the formula.
2. P = 4s
3. P = 4(10) = 40
4. The perimeter of the rhombus is 40.

Example Problem 2

A rhombus shaped table is measured to have a perimeter of 192 cm. What is the length of one of the table's sides?

Solution:

1. Let's plug the perimeter into the equation and solve for side length.
2. P = 4s
3. 192 = 4s, s = ¹⁹²/₄
4. s = 48 cm.
5. The table's side length is 48 cm.