The Perimeter Formulas

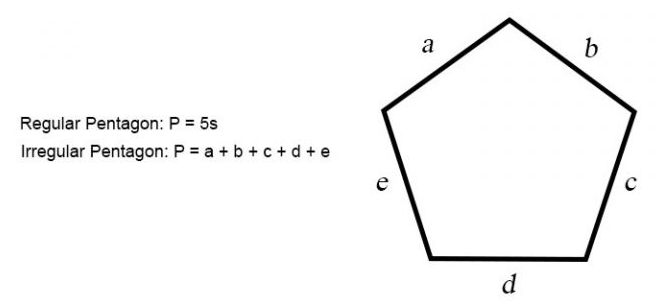
There are two formulas for finding perimeter of a pentagon. For a regular pentagon where all sides are the same length, the formula is given as:
P = 5s
Where P is the perimeter and s is the side length.

For an irregular pentagon where the sides are not all the same length, the formula is given as:
P = a + b + c + d + e
Where a → e are the lengths of each side.

Perimeter of a Pentagon Example Problems

Let's go through a couple of example problems together to practice finding the perimeter of a pentagon.

Example Problem 1

Find the perimeter of a regular pentagon with a side length of 15.

Solution:

1. Since we know this is a regular pentagon, we can plug the side length 15 into the regular pentagon formula.
2. P = 5s
3. P = 5(15) = 75
4. The perimeter is 75.

Example Problem 2

In irregular pentagon has side lengths a = 2.36, b = 4.01, c = 3.12, d = 3.22, and e = 4.41. What is the perimeter?

Solution:

1. Let's plug the side lengths into the irregular pentagon formula.
2. P = a + b + c + d + e
3. P = 2.36 + 4.01 + 3.12 + 3.22 + 4.41 = 17.12
4. The perimeter is 17.12.