How to Find the Perimeter of a Circle

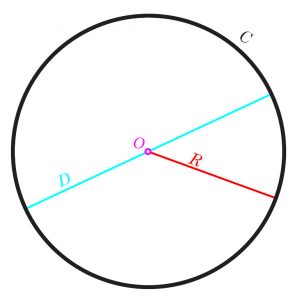
The perimeter of a circle is called the circumference. The formula for perimeter of a circle is the circumference formula. It is given as:

C = 2πr

or:

C = πd

Where C is the circumference, r is the radius of the circle, and d is the diameter of the circle.

Here is an example of using this formula to find circumference of a circle with a radius of 3:

C = 2π(3) = 6π, circumference = 6π.

Perimeter of a Circle Example Problems

Let's go through a couple of example problems together to practice finding the perimeter of a circle.

Example Problem 1

Find the circumference of a circle with a radius of 10.

Solution:

1. Let's plug the radius into the circumference formula.
2. C = 2πr = 2π(10) = 20π
3. The circumference is 20π.

Example Problem 2

Find the circumference of a circle with a diameter of 10.

Solution:

1. Let's plug the diameter into the circumference formula.
2. C = πd = π(10) = 10π
3. The perimeter is 10π.

Example Problem 3

Compare the perimeter of a circle with a diameter of 7 to a square with a side length of 7. The formula for perimeter of a square is P = 4s.

Solution:

1. Let's plug the circle's diameter into the circumference formula. Solving for circumference gives us the perimeter.
2. C = πd = π(7) = 7π.
3. Now let's do the same for the square.
4. C = 4s = 4(7) = 28
5. The circle's perimeter is 7π (≈22) and the square's perimeter is 28.