Two Methods for Finding Height

There are two basic methods we can use to find the height of a triangle. They are given as:

1. If we know the area and base of the triangle, the formula h = ^2A⁄_b can be used.
2. If we know side lengths and angles of the triangle, we can use trigonometry to find height.

Using Area to Find the Height

The area formula for a triangle is A = ¹⁄₂bh. After rearranging the formula to isolate h, we end up with h = ^2A⁄_b. If we have the area and base, we simply plug them into this new formula to find height.

Example Problem:

Find the height of a triangle with a base of 10 and an area of 20.

Solution:

1. Let's use the base and area formula to find the height.
2. Plugging the values in to the formula, we get:
   h = ^2A⁄_b = ²⁽²⁰⁾⁄₍₁₀₎ = 4.
3. The height of the triangle is 4.
   We can check our solution by plugging the height in to the triangle area formula, A = ¹⁄₂bh.
   20 = ¹⁄₂(10)(4), 20 = 20 ✓.

Using Trigonometry to Find the Height

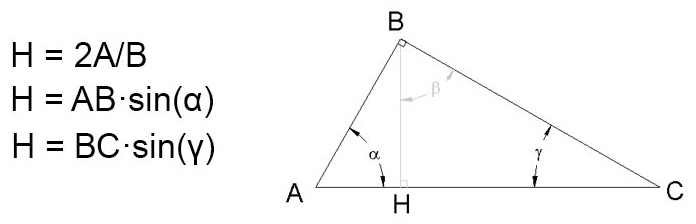
Let's consider the image of the triangle above. There are three labeled sides and three labeled angles. The height is the vertical line labeled H.

The bottom side AC is perfectly horizontal. Since the height is vertical, AC and H are perpendicular. Now, remember that the vertical projection of an angled line is its length times the sine of the line's angle off the horizontal.

Using this relation, we can find the height of the triangle by using side AB or side BC. For the triangle above, the two possible trig formulas for height are given as:

1. h = ABsin(α)
2. h = BCsin(γ)

Example Problem:

In the triangle above, side BC is 7 long and angle γ is 45°. What is the height?

Solution:

1. Plugging the given values into the formula, we get:
   h = BCsin(γ)
   h = (7)sin(45°) = (7)(.7071) = 4.950
2. The height is 4.950.