What is the Distance Formula?

The distance formula is a way of finding the distance between two points. It does this by creating a virtual right triangle and using the Pythagorean theorem. The distance formula has a 2D (two-dimensional) variation and a 3D (three-dimensional) variation.

The 2D distance formula is given as:

$$\begin{align}& d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \end{align}$$

The 3D distance formula is given as:

$$\begin{align}& d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} + (z_{2} - z_{1})^{2}} \end{align}$$

Where d is the distance between the points, (x₁, y₁, z₁) is point 1, and (x₂, y₂, z₂) is point 2.

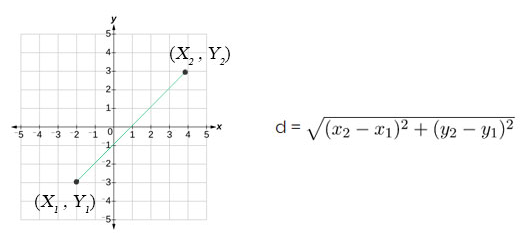
How the Distance Formula Works

The 2D distance formula is the Pythagorean formula applied to two points in the x-y coordinate plane. The first component inside of the square root is (x₂ - x₁)². This is the horizontal leg of the right triangle. The second component inside the square root is (y₂ - y₁)². This is the vertical leg of the right triangle.

We can visualize the 3D distance formula as a right triangle that happens to reside in the x-y-z 3D coordinate system. Because the two points we are measuring between do not sit flat on a 2D plane, we add in the third term with the variable z. The third term inside of the square root is (z₂ - z₁)². It allows the distance between the points to be accurately calculated when they are in 3D space.

2D Distance Formula Example Problem

Find the distance between the points (2, 5) and (7, 3).

Solution:

$$\begin{align}& \text{1.) The points lie in a 2D system/plane. So, we will use the 2D formula.} \\ \\ & \text{2.) Let's substitute the points into the equation and then simplify.} \\ \\ & \text{3.) } d = \sqrt{(7 - 2)^{2} + (3 - 5)^{2}} \\ \\ & \text{4.) } d = \sqrt{(5)^{2} + (-2)^{2}} \\ \\ & \text{5.) } d = \sqrt{25 + 4} \\ \\ & \text{6.) The distance between the points is: } \; \boxed{d = \sqrt{29}} \end{align}$$

3D Distance Formula Example Problem

Find the distance between the points (1, 4, 11) and (2, 6, 18).

Solution:

$$\begin{align}& \text{1.) The points are in 3D space, so we will use the 3D distance formula..} \\ \\ & \text{2.) Let's substitute the points into the equation and then simplify.} \\ \\ & \text{3.) } d = \sqrt{(2 - 1)^{2} + (6 - 4)^{2} + (18 - 11)^{2}} \\ \\ & \text{4.) } d = \sqrt{(1)^{2} + (2)^{2} + (7)^{2}} \\ \\ & \text{5.) } d = \sqrt{1 + 4 + 49} \\ \\ & \text{6.) The distance between the points is: } \; \boxed{d = \sqrt{54}} \end{align}$$