Area of a Triangle Lesson
Triangle Area Formula
The formula for area of a triangle is given as:
A = 1⁄2bh
Where A is the area, b is the base, and h is the height.
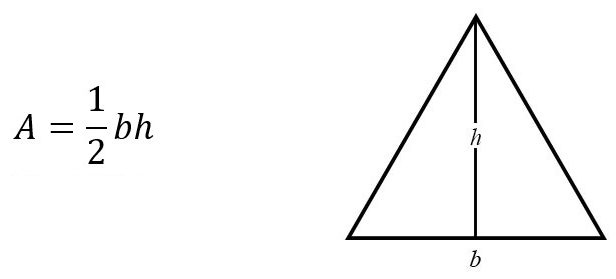
INTRODUCING

Area of a Triangle Example Problems
Let's go through a couple of example problems together to practice finding the area of a triangle.
Example Problem 1
Find the area of a triangle with a base of 10 and a height of 5.
Solution:
- Let's plug the given dimensions into the formula.
- A = 1⁄2bh
- A = 1⁄2(10)(5) = 25
- The area is 25.
Example Problem 2
A triangle's area is measured to be 4.5 square meters and it has an equal base and height. What is the height in meters?
Solution:
- Let's equate the base and height so that we can substitute height in for base.
- b = h
- bh = h2
- Now we can plug the given value into the formula and solve for the height h.
- A = 1⁄2h2
- 4.5 = 1⁄2h2
- 9 = h2
- h = 3
- The height is 3 meters.

