Area of a Sector Lesson
Sector Area Formula
There are two sector area formulas; one for a sector measured in radians, and another for a sector measured in degrees. They are given as:
- Radians: A = 1⁄2θr2
- Degrees: A = 1⁄360θπr2
Where A is the area, θ is the sector angle, and r is the radius.
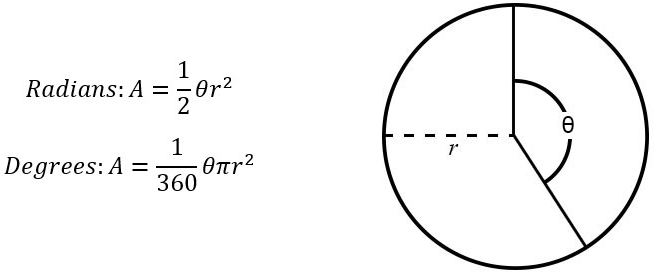
INTRODUCING

Area of a Sector Example Problems
Let's work through a couple of example problems together to practice finding the area of a sector.
Example Problem 1
Find the area of a sector with an angle of 90 degrees and a radius of 10.
Solution:
- Plugging the given dimensions into the formula, we get:
A = 1⁄360θπr2
A = 1⁄360(90)π(102) = 25π - The area is 25π.
Example Problem 2
The sector from problem 1 is changed so that the diameter is 10 instead of the radius being 10. What is the new area?
Solution:
- First, let's convert diameter to radius.
2r = d
2r = 10
r = 5 - Now let's plug the radius and angle into the formula.
A = 1⁄360θπr2
A = 1⁄360(90)π(52) = 6.25π - The area is now 6.25π.

