Menu
Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
Area of a Rectangle
Rectangle Area Formula
The formula for area of a rectangle is given as:
A = bh
Where A is the area, b is the base, and h is the height. We can tip the rectangle over and change which side we use for the base and height as long as the base and height are perpendicular sides.
See the image below for how the base and height of a rectangle are related to each other.
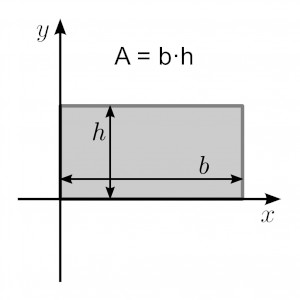
How to Label a Rectangle
The image above has the height axis parallel to the y-axis, and the base axis parallel to the x-axis. This is generally how we want to label a rectangle when calculating area. However, we could rotate the rectangle 90 degrees and will still get the same area.
Also, note that a square is considered a rectangle when calculating area. A square is a rectangle with equal base and height.
Example Problems
Problem 1:
A rectangle has a base of 5 and a height of 7. What is the area of the rectangle?
Solution:
1.) Plugging the base and height into our area formula, we get:
A = bh
A = (5)(7) = 35.
2.) The area of the rectangle is 35.
Problem 2:
A rectangle’s area is measured to be 9 square meters and it has a base of 2 meters. What is the height in meters?
Solution:
1.) Let’s plug the given dimensions into the area formula and then solve for the height h.
A = bh
9 = (2)h
h = 9/2
2.) The height is 9⁄2 meters.
