Pentagon Area Formulas

A regular pentagon has 5 equal sides. There are three simple formulas for finding area of a regular pentagon. They are given as:

1. A = 0.25s²√(25 + 10√5)
2. A = 2.5sa
3. A = 0.5pa

Where A is the area, s is the side length, a is the apothem length, and p is the perimeter.

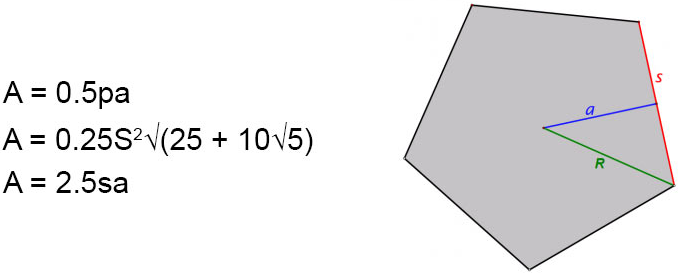
The image below is a regular pentagon, where R is the circumscribing circle radius, a is the apothem, and s is the side length. These dimensions will be useful to reference throughout this lesson.

Using Side Length to Find Area

If we know the side length of a pentagon, we can use the side length formula to find area. The formula is given as:

A = 0.25s²√(25 + 10√5)

Where s is the side length.

Here's an example of using this formula for a pentagon with a side length of 3:

1. A = 0.25s²√(25 + 10√5)
2. A = 0.25(3²)√(25 + 10√5) = (2.25)√(47.36) = 15.48

Using Side Length and Apothem to Find Area

If we know the side length and apothem length, we may use the formula that uses both values. It is much shorter and simpler than the side length area formula. This formula is given as:

A = 2.5sa

Where s is the side length and a is the apothem length.

Using Perimeter and Apothem to Find Area

If we instead know the perimeter and apothem length of a pentagon, we may use the applicable formula. It is given as:

A = 0.5pa

Where p is the perimeter and a is the apothem length.