Area of a Parallelogram

Parallelogram Area Formula

A parallelogram is a quadrilateral with two pairs of parallel sides. The formula for area of a parallelogram is given as:
A = bh
Where A is the area, b is the base, and h is the height.

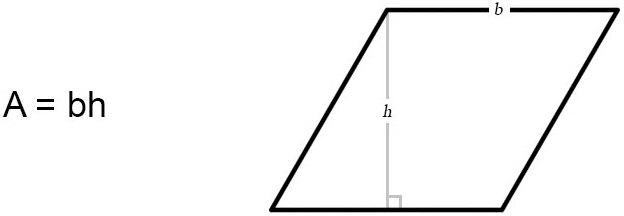
But wait, isn’t that just the area formula for a rectangle?

That’s correct. The formula for area of a parallelogram is the same as the one for area of a rectangle. A parallelogram is actually a rectangle with opposing right triangles on the sides. The triangles are flipped upside down from each other so that the opposing sides are parallel.

Check out the awesome GIF below to see how the rectangle and two right triangles combine to make a parallelogram.

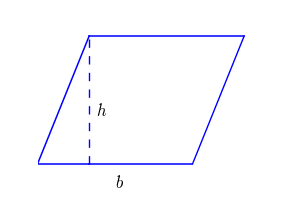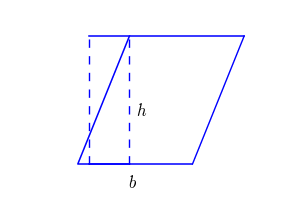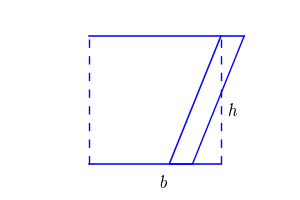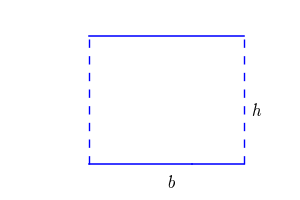
From the GIF above, we can hopefully see why parallelograms and rectangles share the same area formula.

Remember that the definition of a parallelogram is “a four sided, 2-D shape with opposite sides parallel.”

If we come across a shape that looks like a rectangle with two triangles attached, it is not guaranteed to be a parallelogram, since the triangles could have different angles. The opposite sides must be parallel to each other for it to be considered a parallelogram.

Example Problem

Find the area of a parallelogram with a height of 12 and a base of 4.
Solution:
1.) We are given the base and height of the shape, so let’s plug them into the area formula.
2.) A = bh
A = (4)(12) = 48
3.) The area of the parallelogram is 48.