Area of a Kite

Kite Area Formula

A kite is a quadrilateral with two pairs of equal-length sides. The equal length sides are always opposite each other. There are two simple formulas for finding the area of a kite. They are given as:
1.) A = d₁d₂/2
2.) A = absin(c)
Where A is the area, d₁ is the long diagonal, d₂ is the short diagonal, a is the short side, b is the long side, and c is the angle between short and long sides.

The diagonals method can be considered the simpler of the two because it only involves two basic length values. The trigonometry method requires us to know the angle between unequal sides. See the image below for how these dimensions within a kite are notated.

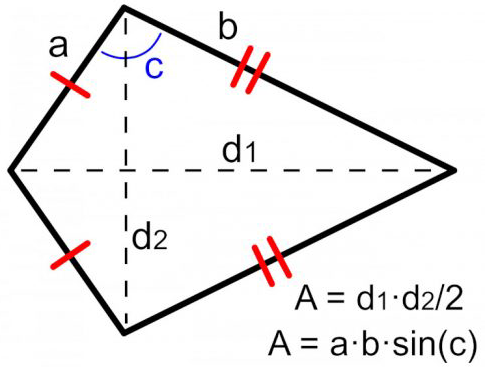
Formula 1: Using the Diagonals to Find Area

If we know the diagonals of a kite, we can use the diagonals formula to find area. The formula is given as:
A = d₁d₂/2
Where d₁ is the long diagonal and d₂ is the short diagonal.

Here’s an example of using this formula for a kite with a long diagonal length of 4 and short diagonal length of 2.
A = d₁d₂/2
A = (4)(2)/2 = 8/2 = 4

Formula 2: Using Trigonometry to Find Area

If we know the side lengths and angle between unequal sides, we can use trigonometry to find area of a kite. The formula for this is given as:
A = absin(c)
Where a is the length of the short side, b is the length of the long side, and c is the internal angle between those two sides.
Here’s an example of using this formula for a kite with a side a length of 4, a side b length of 7, and an internal angle c value of 100 degrees.
A = absin(c)
A = (4)(7)sin(100°) = (28)(0.9848) = 27.574