Area of a Hexagon

Hexagon Area Formula

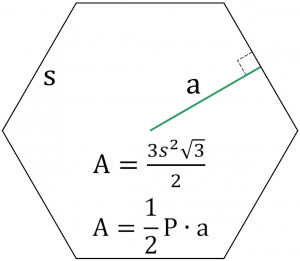
A regular hexagon has 6 equal sides. There are two simple formulas for finding area of a regular hexagon. They are given as:
1.) A = ³⁄₂s²√3
2.) A = ¹⁄₂Pa
Where A is the area, s is the side length, P is the perimeter, and a is the apothem length.

We will go through each of the two formulas in this lesson. Both formulas calculate the area accurately. We can pick which one to use based on what information is given when we are faced with finding the area of a regular hexagon.

Formula 1: Using Side Length

If we know the side length of a regular hexagon, we can plug it straight into the side length area formula. The formula for area of a hexagon using side length is given as:
A = ³⁄₂s²√3
Where A is the area and s is the side length.

Here’s an example of using the side length formula for a hexagon with a side length of 6:
A = ³⁄₂(6²)√3 = 54√3 = 93.531

Formula 2: Using Apothem and Perimeter

If we know the apothem length and perimeter of a regular hexagon, we can use the apothem and perimeter formula for area. The formula is given as:
A = ¹/₂Pa
Where A is the area, a is the apothem length, and P is the perimeter of the hexagon. The apothem length is measured as a right angle from the side of a hexagon to its center.

Here’s an example of using this formula for a hexagon with an apothem length of 3 and a perimeter of 20.785:
A = ¹/₂(20.785)(3) = 31.178