What is an Interval of Convergence?

For a power series, the interval of convergence is the interval in which the series has absolute convergence. It is expressed in interval notation. For example, a series that converges between 2 (inclusive) and 8 (exclusive) may be written as [2, 8) or as 2 < x < 8.

A power series is an infinite series of the form:

$$\sum\limits_{n = 0}^\infty {{c_n}{{\left( {x - a} \right)}^n}}$$

Where c_n is a coefficient that varies with n and the series is a function of x with its terms varying with the n^th term of the series.

Let's look further into the meaning of convergence in the context of a power series. A power series adds an infinite number of successive terms. The sum of those terms can either be finite or infinite.

The series converges if the sum of those terms is a finite number. The series diverges if the sum of those terms is infinite. By solving for the interval of convergence, we find the range of values for x in |x - a| < R such that the series converges.

Why do we Learn Interval of Convergence?

Compared to humans, computers are really good at certain types of calculations but have difficulties performing other types of calculations. For example, the seemingly simple e^x button commonly found on hand calculators is one that the calculator's computer cannot easily and accurately solve directly.

By learning how to find the interval of convergence, we can program an otherwise incapable computer to indirectly find the value of e^x via use of a power series.

If we are evaluating e^x with a large exponent, a calculator's computer has to multiply large, messy numbers by large, messy numbers many times over. Because of how computers store floating-point numbers and create round-off error, this process can take the computer very long and can give an inaccurate answer.

Luckily, the power series f(x) = ^xn⁄_n! represents the expression e^x when carried out to many terms. If we check the interval of convergence for this power series, we find that it is ∞ < x < ∞. This is great news because it means the power series will converge everywhere and can be used for e^x with all possible input x values.

By programming this routine into a computer, we enable it to quickly and accurately solve for the value of e^x with any value of x. This is just one example of a use for the interval of convergence, and there are many more applications that work behind the scenes inside computer software to help us every day!

Calculating the Interval of Convergence of a Power Series

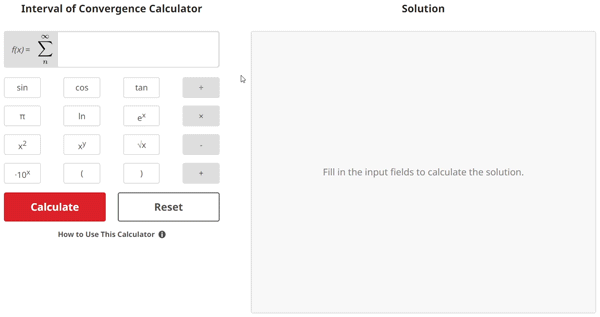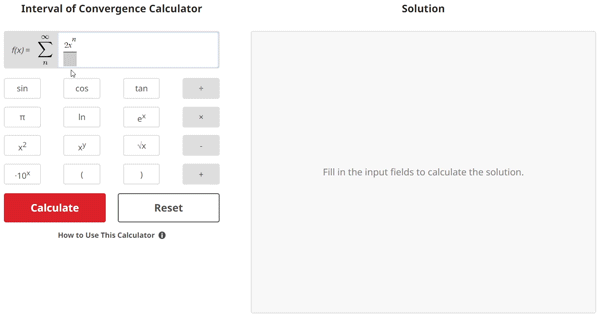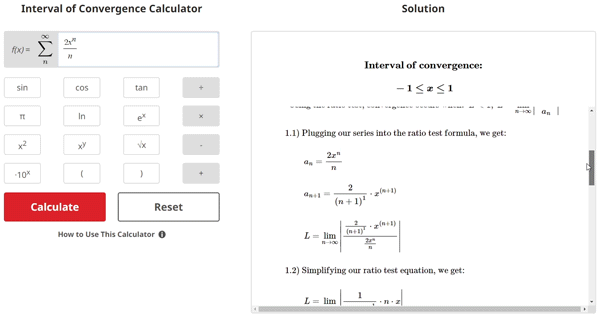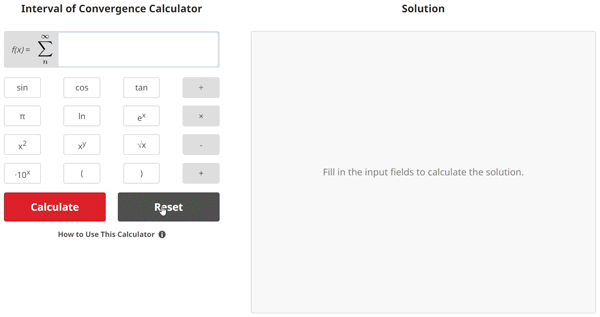
When solving for convergence of a power series, we have multiple test options to choose from. These include the very common ratio test and root test. Since the ratio test is user-friendly and used by the calculator on this page, we learn how to use it here.

With the ratio test, we use a ratio of the power series and a modified n + 1 version of itself to solve for the values of x that satisfy the convergence criteria. The formula for the ratio test is:

$$\text{Convergence when} \; L < 1, \; L = \lim_{n\to\infty} \left\lvert\frac{a_{n+1}}{a_{n}} \right\rvert$$

Where a_n is the power series and a_{n + 1} is the power series with all terms n replaced with n + 1.

The first step of the ratio test is to plug the original and modified versions of the power series into their respective locations in the formula. We may simplify the resulting fraction.

Then, evaluate the limit as n approaches infinity. By plugging infinity in for n, the expression may become what appears to be unsolvable. We then start cancelling out terms that are insignificant compared to infinity and eliminate the actual infinity terms from the expression.

After evaluating the limit and simplifying the resultant expression, set up the expression such that L < 1. We now have an inequality resembling the form of ¹⁄_c×|x - a| < 1. The constant c can be fractional or non-fractional.

Solve for the left and right endpoint that satisfy the final inequality. Those are the interval of convergence bounds. We must determine if each bound is inclusive or exclusive. To do this, we check for series convergence/divergence at those points.

Plug the left endpoint value x = a₁ in for x in the original power series. Then, take the limit as n approaches infinity. If the result is nonzero or undefined, the series diverges at that point. Divergence indicates an exclusive endpoint and convergence indicates an inclusive endpoint. Repeat the process for the right endpoint x = a₂ to complete the interval of convergence.

How the Calculator Works

This interval of convergence calculator is primarily written in JavaScript (JS). Because the computation routine is JS, it runs entirely in your browser in real-time. This allows near-instant solutions and avoids the usual page reloads seen on other calculator websites.

The computation routine also utilizes a JS-native computer algebra system (CAS). The CAS performs various symbolic operations throughout the routine, such as polynomial division and limit evaluation.

The routine itself is exactly the same as explained in this lesson. It uses the ratio test by filling out the formula with your inputted power series. Various states of the expression are saved along the way and used for the solution steps. The answer and solution steps are procedurally built out and rendered as LaTeX code (a math rendering language).