How do you Differentiate Arctangent?

The inverse tangent - known as arctangent or shorthand as arctan, is usually notated as tan^-1(some function). To differentiate it quickly, we have two options:

1. Use the simple derivative rule.
2. Derive the derivative rule, and then apply the rule.

In this lesson, we show the derivative rule for tan^-1(u) and tan^-1(x). Additionally, we cover how the derivative rule is derived.

At the end of the lesson, there are four example problems to help with your understanding of this subject.

Derivative of Arctan(u)

The derivative rule for arctan(u) is given as:

$$\begin{align} & [tan^{-1}(u)]' = \frac{u'}{1+u^{2}} \end{align}$$

Where u is a function of a single variable, and the prime symbol ' denotes the derivative with respect to that variable. Here are some examples of a single variable function u:

• u = x
• u = sin(x)
• u = y³ - 3y + 4

Derivative of Arctan(x)

The derivative rule for arctan(x) is the arctan(u) rule but with each instance of u replaced by x. Since the derivative of x is 1, the numerator simplifies to 1. The derivative rule for arctan(x) is given as:

$$\begin{align} & [tan^{-1}(x)]' = \frac{1}{1+x^{2}} \end{align}$$

Where ' denotes the derivative with respect to x.

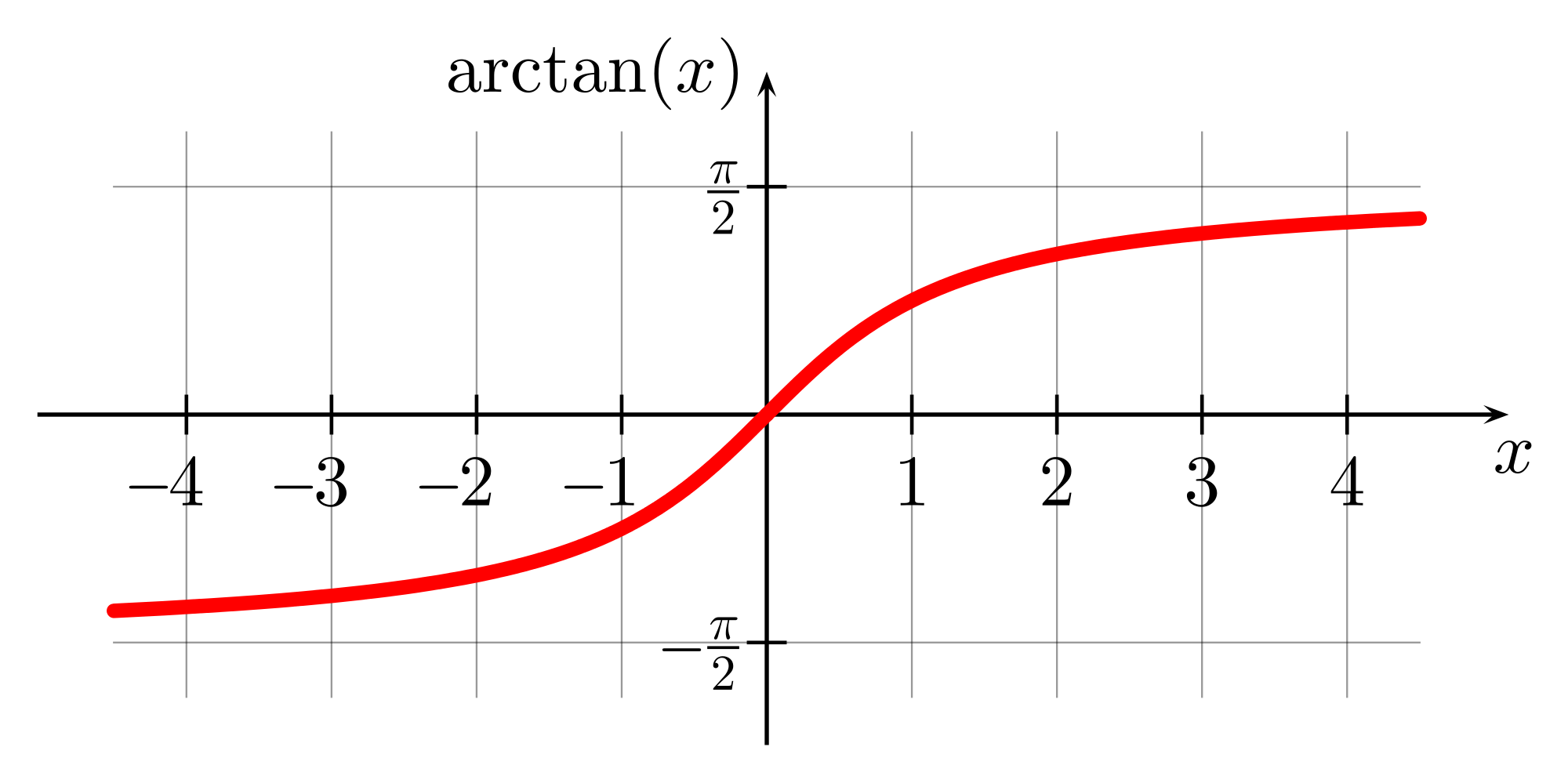
What Makes Arctan Differentiable?

Arctan is a differentiable function because its derivative exists on every point of its domain. In the image below, a single period of arctan(x) is shown graphed. The curve is continuous and does not have any sharp corners.

If there is a sharp corner on a graph, the derivative is not defined at that point. So, if you come across a function whose graph has sharp corners, it will not be differentiable on every point of its domain.

Proof of the Derivative Rule

Since arctangent means inverse tangent, we know that arctangent is the inverse function of tangent. Therefore, we may prove the derivative of arctan(x) by relating it as an inverse function of tangent. Here are the steps for deriving the arctan(x) derivative rule.

1. y = arctan(x), so x = tan(y)
2. ^dx⁄_dy[x = tan(y)] = sec²(y)
3. Using sum of squares corollary: sec²(y) = 1 + tan²(y)
4. tan²(y) = x², so ^dx⁄_dy = 1 + x²
5. Flipping ^dx⁄_dy, we get ^dy⁄_dx = ¹⁄_{(1 + x²)}

Derivative of Arctan Example Problems

Derivative of Arctan(2x)

$$\begin{align} & \text{Find the derivative of } tan^{-1}(2x) \text{ with respect to } x \text{.} \\ \\ & \text{Solution:} \\ \\ & \text{1.) Let's set } u = 2x \\ \\ & \text{2.) } u' = 2 \\ \\ & \text{3.) } u^{2} = 4x^{2} \\ \\ & \text{4.) } \frac{d}{dx}\left[tan^{-1}(2x)\right] = \frac{2}{1+4x^{2}} \\ \\ & \Rightarrow \text{The solution is } \frac{2}{1+4x^{2}} \end{align}$$

Derivative of Arctan(¹⁄_x)

$$\begin{align} & \text{Find the derivative of } tan^{-1}\left(\frac{1}{x}\right) \text{ with respect to } x \text{.} \\ \\ & \text{Solution:} \\ \\ & \text{1.) Let's set } u = \frac{1}{x} \\ \\ & \text{2.) } u' = -\frac{1}{x^{2}} \\ \\ & \text{3.) } u^{2} = \frac{1}{x^{2}} \\ \\ & \text{4.) } \frac{d}{dx}\left[tan^{-1}\left(\frac{1}{x}\right)\right] = \frac{-\frac{1}{x^{2}}}{1+\frac{1}{x^{2}}} \\ \\ & \text{5.) Simplify: } \frac{-\frac{1}{x^{2}}}{1+\frac{1}{x^{2}}} \cdot \frac{x^{2}}{x^{2}} = -\frac{1}{x^{2}+1} \\ \\ & \Rightarrow \text{The solution is } -\frac{1}{x^{2}+1} \end{align}$$

Derivative of Arctan(4x)

$$\begin{align} & \text{Find the derivative of } tan^{-1}\left(4x\right) \text{ with respect to } x \text{.} \\ \\ & \text{Solution:} \\ \\ & \text{1.) Let's set } u = 4x \\ \\ & \text{2.) } u' = 4 \\ \\ & \text{3.) } u^{2} = 16x^{2} \\ \\ & \text{4.) } \frac{d}{dx}\left[tan^{-1}\left(4x\right)\right] = \frac{4}{1+16x^{2}} \\ \\ & \Rightarrow \text{The solution is } \frac{4}{1+16x^{2}} \end{align}$$

Derivative of Arctan(x² + 1)

$$\begin{align} & \text{Find the derivative of } tan^{-1}\left(x^{2}+1\right) \text{ with respect to } x \text{.} \\ \\ & \text{Solution:} \\ \\ & \text{1.) Let's set } u = x^{2}+1 \\ \\ & \text{2.) } u' = 2x \\ \\ & \text{3.) } u^{2} = \left(x^{2}+1\right)\left(x^{2}+1\right) = x^{4}+2x^{2}+1 \\ \\ & \text{4.) } \frac{d}{dx}\left[tan^{-1}\left(x^{2}+1\right)\right] = \frac{2x}{1+x^{4}+2x^{2}+1} \\ \\ & \text{5.) Simplify: } \frac{d}{dx}\left[tan^{-1}\left(x^{2}+1\right)\right] = \frac{2x}{x^{4}+2x^{2}+2} \\ \\ & \Rightarrow \text{The solution is } \frac{2x}{x^{4}+2x^{2}+2} \end{align}$$