What is Point Slope Form?

The equation of a line can be displayed in various formats such as slope-intercept form (y = mx + b), or in the case of this lesson, point-slope form.

Point-slope form is the equation of a line given in the following format:

$$y-y_{1}=m(x-x_{1})$$

Where m is the slope of the line and (x₁,y₁) is a point that the line passes through.

In other words, point-slope form is a way of representing the equation of a line passing through a point.

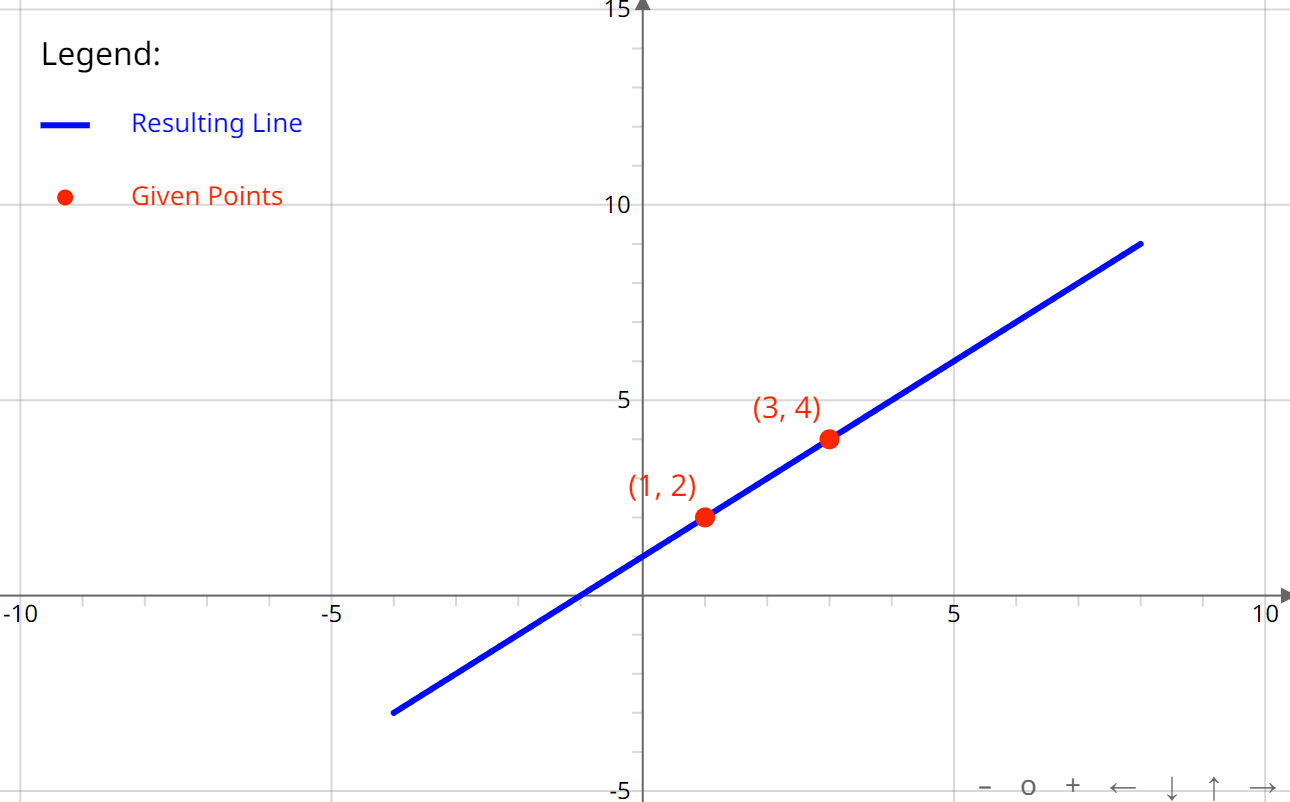
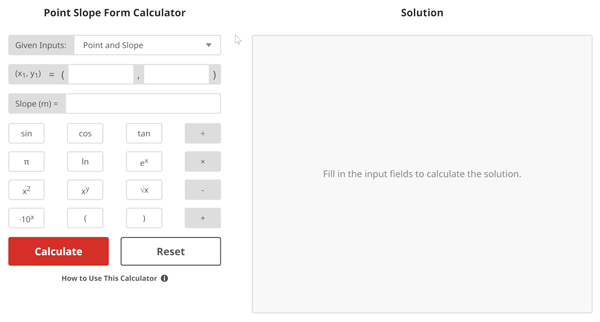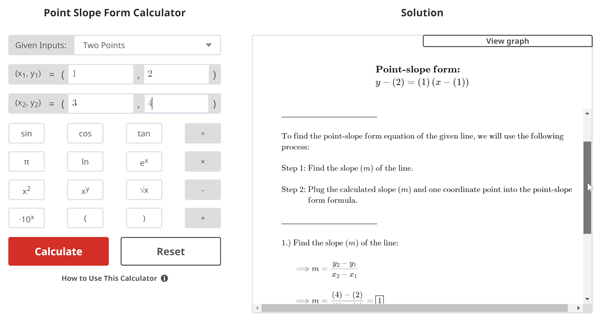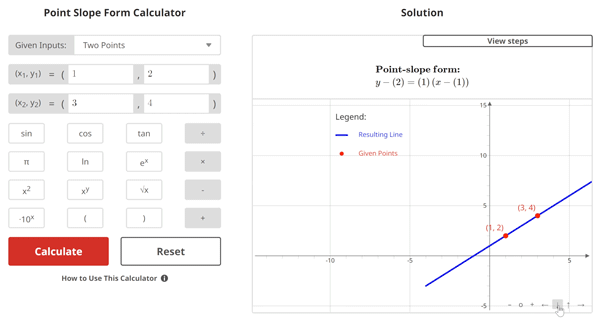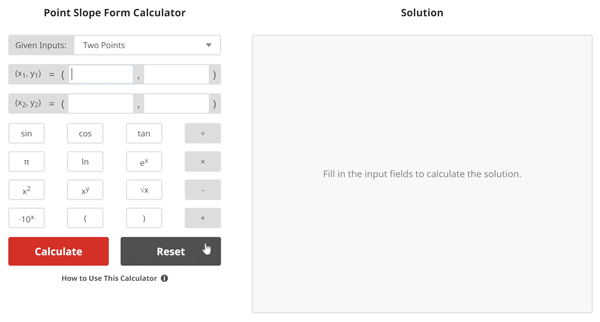
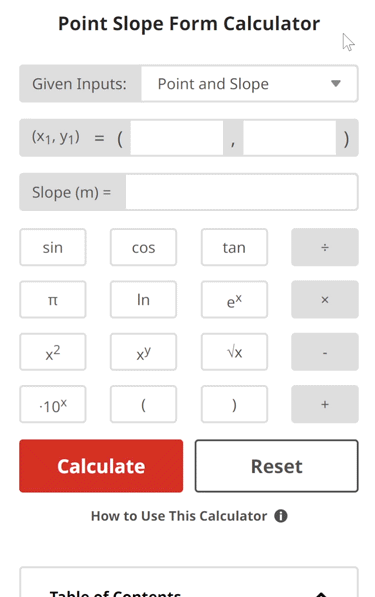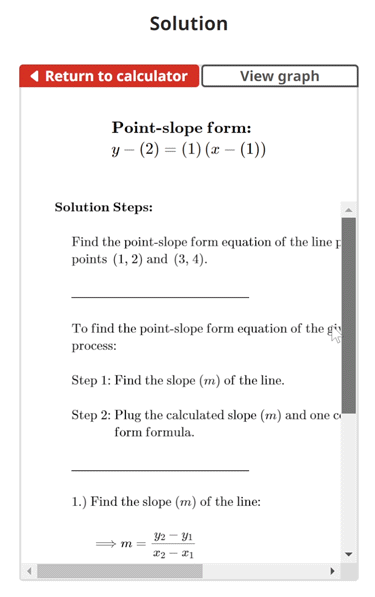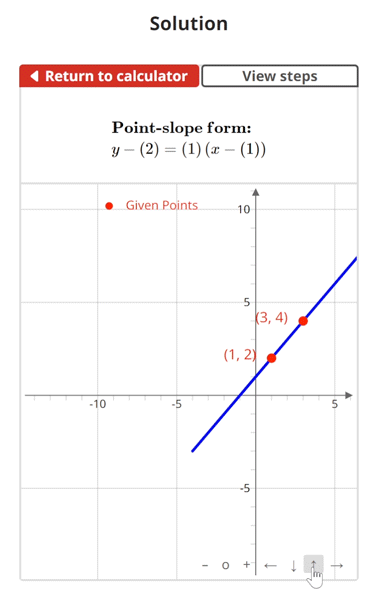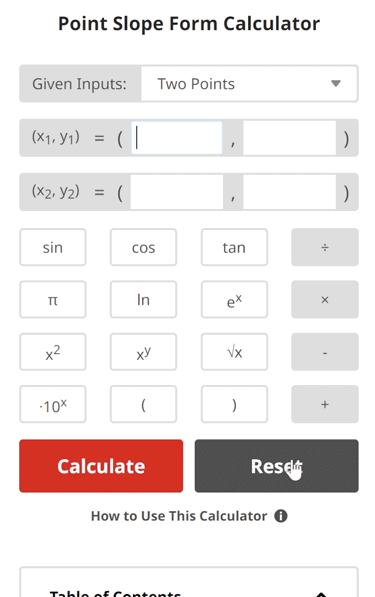
Figure 1 is an example of a line that passes through points (1,2) and (3,4). The equation of the line written in point-slope from is y - (2) = (1)(x - (1)).

Why do we Learn About Point Slope Form?

As simple as they might seem, lines (and their equations) can characterize things like revenue growth in a business over time, or how much money will be in our bank accounts if we continue saving a steady amount of money every month.

For example, let's say that you steadily save the same amount of money each month for your favorite hobby.

If you were to chart out the money saved (y-axis) with respect to time (x-axis), you'd likely see a line (or line-shaped) upward trend. By characterizing this line with its respective equation, you'd be able to quickly estimate how much money would be saved after an arbitrary amount of time by changing the time variable (x) and calculating.

This is just one of many different ways that understanding point-slope form, as well as the other formats for the equation of a line, can help us in our day-to-day lives.

How to Find the Point Slope Form Equation of a Line

To find the point-slope form equation of a line, plug the slope (m) and point (x₁,y₁) into the point-slope form formula.

$$y-y_{1}=m(x-x_{1})$$

If we are given two points rather than one point and the slope, we can calculate the slope of a line (m) by using the following formula:

$$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$

Point Slope Form Example Problem

$$\begin{align}& \textbf{Solution Steps:} \hspace{62ex} \\ \\ & \hspace{3ex} \text{Find the point-slope form equation of the line passing through the coordinate} \\ & \hspace{3ex}\text{points }\left(1\text{, }2\right) \text{ }\text{and }\left(3\text{, }4\right)\text{.}\\ \\ & \hspace{3ex} \rule{6cm}{0.8pt} \\ \\ & \hspace{3ex}\text{To find the point-slope form equation of the given line, we will use the} \\ & \hspace{3ex} \text{following process:} \\ \\ & \hspace{3ex} \text{Step 1: Find the slope (} m \text{) of the line.} \\ \\ & \hspace{3ex} \text{Step 2: Plug the calculated slope (} m \text{) and one coordinate point into the} \\ & \hspace{10.5ex} \text{point-slope form formula.}\\ \\ & \hspace{3ex} \rule{6cm}{0.8pt}\\ \\ & \hspace{3ex} \text{1.) Find the slope (} m \text{) of the line:} \\ \\ & \hspace{6.5ex} \Longrightarrow m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ \\ & \hspace{6.5ex} \Longrightarrow m = \frac{\left(4\right)-\left(2\right)}{\left(3\right)-\left(1\right)} = \boxed{1}\\ \\ & \hspace{3ex} \text{2.) Plug the slope (} m \text{) from Step 1 and the given coordinate point }\left(1\text{, }2\right)\text{ into} \\ & \hspace{6.5ex} \text{the point-slope form formula given below:} \\ \\ & \hspace{6.5ex} \Longrightarrow \text{Point-slope form: } y-y_{1} = m(x-x_{1}) \\ \\ & \hspace{6.5ex} \Longrightarrow \boxed{y-\left(2\right) = \left(1\right)\left(x-\left(1\right)\right)} \\ \\ & \hspace{3ex} \textbf{Therefore, the point-slope form equation of the given line is} \\ & \hspace{3ex} \boldsymbol{y-\left(2\right) = \left(1\right)\left(x-\left(1\right)\right)}\textbf{.}\\ & \end{align}$$

How the Calculator Works

The Point Slope Form Calculator was developed using HTML (Hypertext Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript).

HTML is used to create and name various elements that come together to act as the framework of the calculator.

CSS is used to style the calculator by defining each element's color, size, and other relevant visual properties.

JS is used for the calculator's functionality such as performing the calculation, generating the graph, and resetting the input fields when the "Reset" button is pressed.

This all comes together to provide an easy way for the user to learn about point-slope form.