Menu
Related Content
Thank you!
On behalf of our dedicated team, we thank you for your continued support. It's fulfilling to see so many people using Voovers to find solutions to their problems. Thanks again and we look forward to continue helping you along your journey!
Nikkolas and Alex
Founders and Owners of Voovers
One to One Function
Lesson Contents
What is a One to One Function?
Also known as an injective function, a one to one function is a mathematical function that has only one y value for each x value, and only one x value for each y value.
Let’s take y = 2x as an example. Plugging in a number for x will result in a single output for y. Also, plugging in a number for y will result in a single output for x. Both conditions hold true for the entire domain of y = 2x. Therefore, y = 2x is a one to one function.
Now let’s take y = x2 as an example. Plugging in any number for x along the entire domain will result in a single output for y. However, plugging in any number for y does not always result in a single output for x. For instance, at y = 4, x = 2 and x = -2. Therefore, y = x2 is a function, but not a one to one function.
How to Test if it's a One to One Function
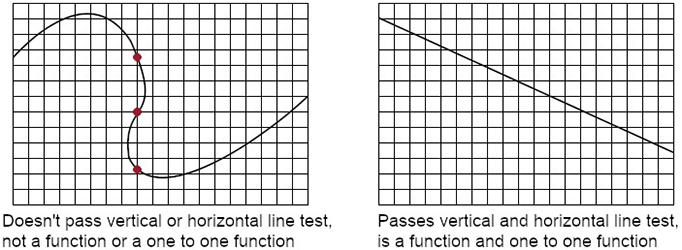
A one to one function passes the vertical line test and the horizontal line test. The first step is to graph the curve or visualize the graph of the curve.
To perform a vertical line test, draw vertical lines that pass through the curve. For the curve to pass the test, each vertical line should only intersect the curve once. Passing the vertical line test means it only has one y value per x value and is a function.
The horizontal line test is the vertical line test but with horizontal lines instead. For the curve to pass, each horizontal should only intersect the curve once. Passing the horizontal line test means it only has one x value per y value.
