What is the Midpoint Formula?

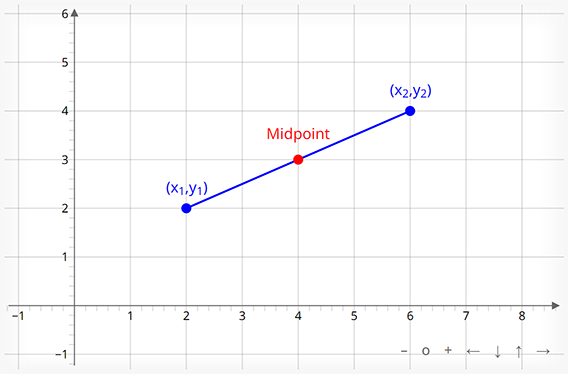
The midpoint formula allows us to find the midpoint of a line between two distinct points. In other words, it takes the average of a line's given endpoints.

Why do we Learn About the Midpoint Formula?

The midpoint formula might be a fundamental topic, but it can be very useful when high tech tools and gadgets are unavailable.

Let's say that we are camping the woods and we want to set up our tent approximately between the lake where we will catch fish and a patch of small trees where we can gather firewood with a small hatchet.

Unfortunately, somewhere between the lake and firewood spot, there is a ravine that is surrounded by large trees that blocks a direct path and line of sight between our two points of interest. Since we only have a watch and a compass, we will have to make use of what we have to navigate to the approximate midpoint between the lake and firewood spot.

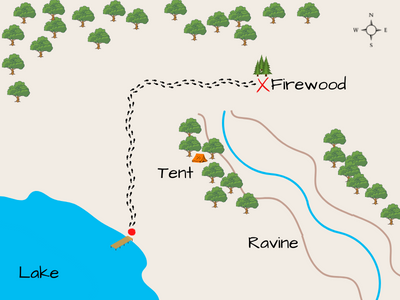
Beginning at the lake, we can begin walking north at a consistent pace until we see the firewood gathering area directly to the east such that the ravine is no longer in our way. At this point we will take a mental note of how long it took us to reach this spot to the north. Then, we can walk to the east until we get to our firewood gathering spot while taking note of the travel time.

Since the lake was our starting point, the coordinates based on travel time will be (0 minutes east, 0 minutes north). Let's say that we walked 10 minutes to the north and 6 minutes to the east to get to the firewood spot from the lake. This would leave us with the travel time coordinates of (6 minutes east, 10 minutes north).

Applying the midpoint formula, we find that we need to walk north for 5 minutes and east for 3 minutes to reach the approximate midpoint between the lake and firewood gathering area where we will set up camp.

How to use the Midpoint Formula

We can find the midpoint of a line by using the following formula:

$$\begin{align} & \left(\frac{(x_{1} + x_{2})}{2}, \frac{(y_{1} + y_{2})}{2}\right)\end{align}$$

Where x₁, y₁, x₂, and y₂ are the given coordinates for the first and second points respectively.

The steps for finding the midpoint are as follows:

1. Add x₁ to x₂.
2. Divide the result from Step 1 by 2 (This is the x coordinate for the midpoint).
3. Add y₁ to y₂.
4. Divide the result from Step 3 by 2 (This is the y coordinate for the midpoint).

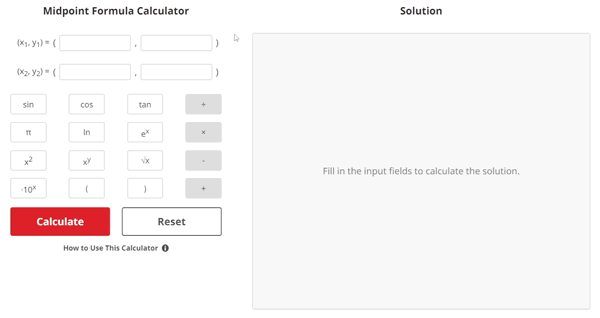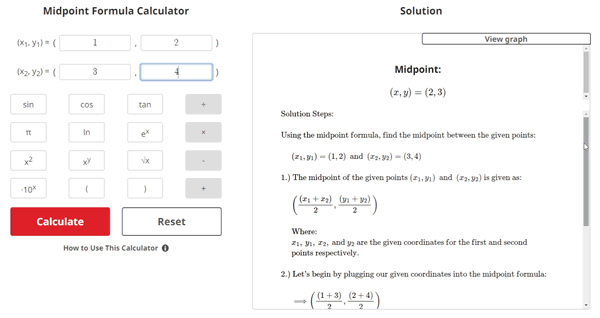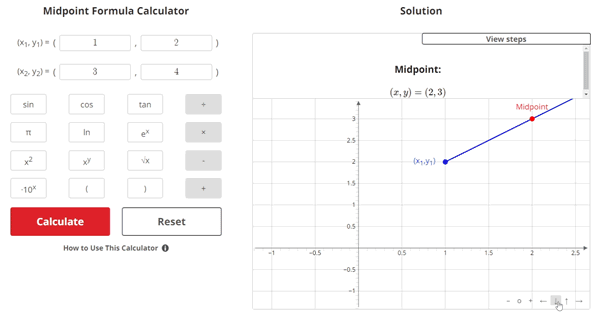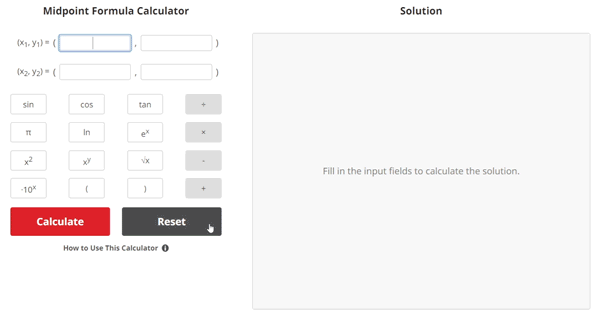
Midpoint Formula Example Problem

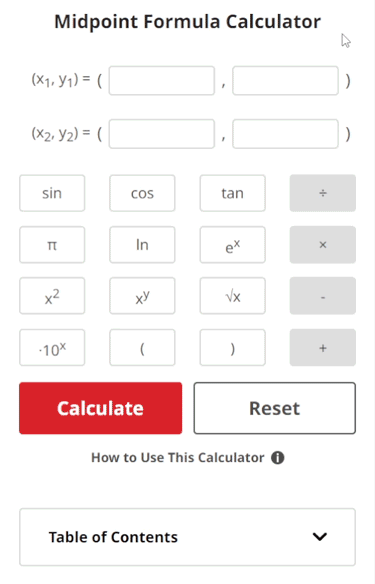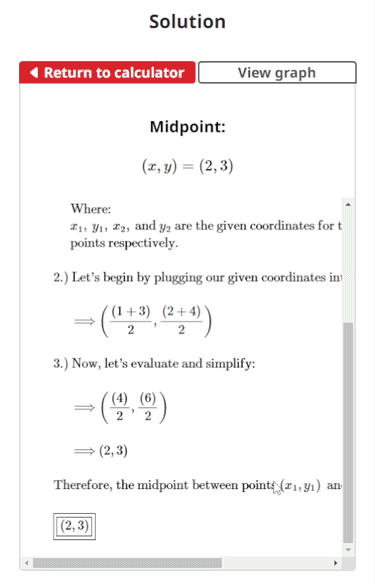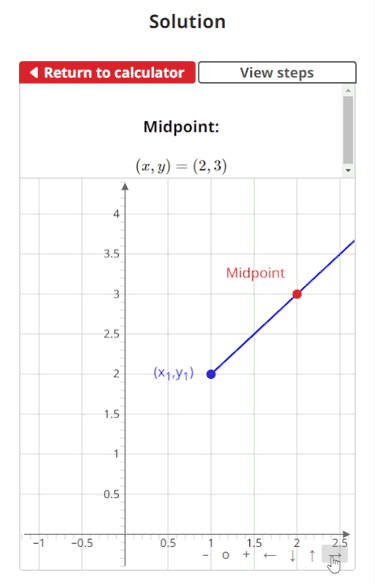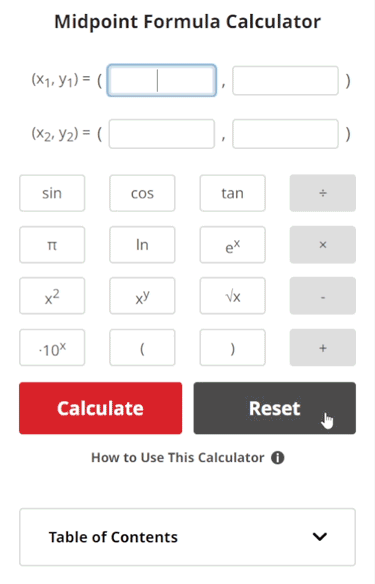
$$\begin{align} & \text{Using the midpoint formula, find the midpoint between the given points:} \\ \\ & \hspace{3ex} (x_{1}, y_{1}) = (1, 2) \: \text{ and } \: (x_{2}, y_{2}) = (3, 4)\\ \\ & \text{1.) The midpoint of the given points } (x_{1}, y_{1}) \: \text{ and } \: (x_{2}, y_{2}) \text{ is given as:} \\ \\ & \hspace{3ex} \left(\frac{(x_{1} + x_{2})}{2}, \frac{(y_{1} + y_{2})}{2}\right) \\ \\ & \hspace{3ex} \text{Where: } \\ & \hspace{3ex} x_{1}, \: y_{1}, \: x_{2},\text{ and } y_{2} \text{ are the given coordinates for the first and second } \\ & \hspace{3ex} \text{points respectively.}\\ \\ & \text{2.) Let's begin by plugging our given coordinates into the midpoint formula:} \\ \\ & \hspace{3ex} \Longrightarrow \left(\frac{(1 + 3)}{2}, \frac{(2 + 4)}{2}\right)\\ \\ & \text{3.) Now, let's evaluate and simplify:} \\ \\ & \hspace{3ex} \Longrightarrow \left(\frac{(4)}{2}, \frac{(6)}{2}\right) \\ \\ & \hspace{3ex} \Longrightarrow (2, 3)\\ \\ & \text{Therefore, the midpoint between points }(x_{1}, y_{1}) \: \text{ and } \: (x_{2}, y_{2}) \text{ is:} \\ \\ & \boxed{\boxed{(2, 3)}}\end{align}$$

How the Calculator Works

The Midpoint Formula Calculator uses a combination of HTML, CSS, and JavaScript.

HTML, or “HyperText Markup Language”, provides the framework for the calculator. With HTML, we can create entities such as the calculator box, solution steps field, and the various buttons on the interface.

We then use CSS, or “Cascading Style Sheets”, for the aesthetic design of the aforementioned calculator, calculator buttons, and solution steps field.

While having the virtual calculator interface on the page is a good start, the calculator has to also be functional. To accomplish this, JS, or “JavaScript”, is used. JS allows the calculator buttons to insert the relevant value into the input fields when pressed. JS also allows the actual mathematical calculations to take place when the "calculate" button is pressed.

All of these elements come together to form the Midpoint Formula Calculator that allows users to find the midpoint between their given endpoints, see solution steps that change based on their inputs, and visualize their problem on an interactive graph.