What is a Horizontal Asymptote?

A horizontal asymptote is a horizontal line that the curve of a function approaches, but never touches, as the x-value of the function becomes either very large, very small, or both very large and very small.

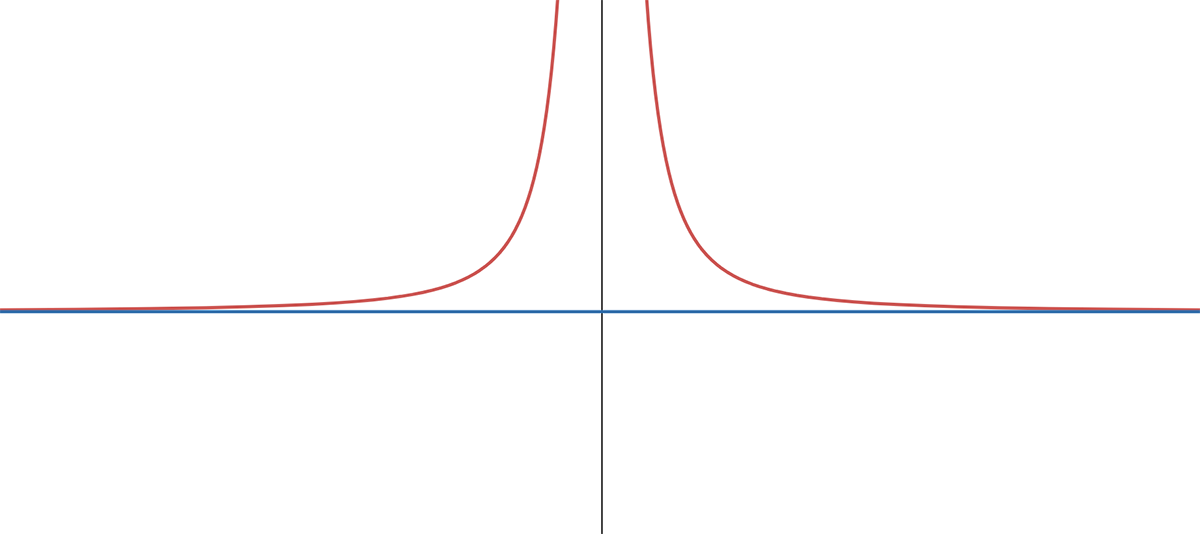
The image below shows an example of a function with a horizontal asymptote. In this case, the graph of the function approaches the horizontal line y = 0, but never touches it, as the x-value of the function becomes very large (positive infinity) and very small (negative infinity). Therefore, it has a horizontal asymptote at y = 0.

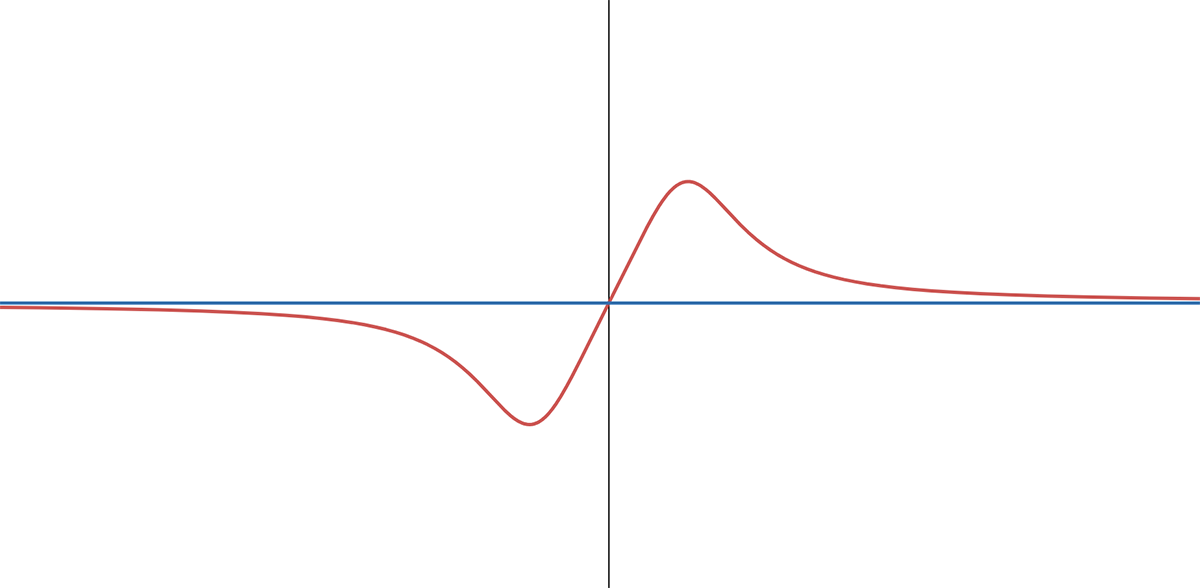
Unlike vertical asymptotes, a horizontal asymptote can be crossed by the function. If a function crosses its horizontal asymptote at some point(s) but still approaches the asymptote as expected at some at very large or small x-values, the asymptote remains valid. The image below shows the graph of a function that exhibits this behavior.

Horizontal asymptotes may occur in rational functions, which are functions that take the form of a polynomial divided by another polynomial. Some examples of rational functions include:

$$\begin{align}& y = \frac{2x-5}{2x^{2}+2} \hspace{5ex} y = \frac{2x^{3}-x^{2}}{(x+2)(x-1)} \\ \\ & y = \frac{x^{4}}{x+50} \hspace{6ex} y = \frac{x(x^{2}-7)}{x-3}\end{align}$$

Horizontal asymptotes may also occur in exponential functions, which are functions with a constant raised to the x power. Some examples of exponential functions include:

$$\begin{align}& y = 5^{x} \hspace{8ex} y = 2^{x} \: - \: 5 \\ \\ & y = -7^{-x} \hspace{5ex} y = -12^{x} + 3\end{align}$$

Why We Learn About Horizontal Asymptotes

Horizontal asymptotes appear in a surprisingly numerous amount of real-world mathematical relations. So, let's take a look at just one of these examples: We can design a space capsule's parachute system by determining the capsule's terminal velocity with a horizontal asymptote calculation.

When an object falls downward through an atmosphere, the force of gravity pulls it downward and accelerates it towards the center of the planet. But, the air in the atmosphere provides a resistance force (called drag) which increases in magnitude as the object's speed increases. As the object gains speed, the rate that it gains speed starts to decrease since the force of drag begins to fight the force of gravity harder and harder.

Eventually, the force of drag becomes so close in magnitude to the force of gravity that the object's downward acceleration approaches zero in magnitude. The object is approaching its highest possible speed but will not reach it since the acceleration is nearing zero in magnitude. This highest possible speed is called the object's terminal velocity.

When the space capsule re-enters the atmosphere after a mission in space, it will exhibit this behavior. The velocity versus time graph of the capsule will have a horizontal asymptote located at velocity = terminal velocity. As time becomes very large, velocity will approach, but never reach this horizontal asymptote.

Since the capsule approaches, but never reaches or exceeds its terminal velocity, we can design its parachute system for a worst-case scenario where it deploys at terminal velocity (with some extra margin of safety above that velocity built-in to the design).

By finding a horizontal asymptote, we have optimized a space capsule parachute system's performance and ensured the crew returns home safely!

How do You Find the Horizontal Asymptotes of a Function?

Rational functions and exponential functions have different methods for finding their horizontal asymptotes, so we will go through them separately.

Finding the Horizontal Asymptotes of a Rational Function

To find the horizontal asymptotes of a rational function, we may use the three steps shown below. We will solve for three different rational functions (example a, example b, and example c) to highlight the process of finding their horizontal asymptotes.

1. Fully expand both the numerator and denominator so there are no quantities inside of any parenthesis left in either of them.

$$\begin{align} & \text{Example a.)} \hspace{2ex} y = \frac{2x(x+3)}{(x^{2}+2)(x-1)} \hspace{2ex} \text{Becomes:} \hspace{2ex} y = \frac{2x^{2}+6x}{x^{3}-x^{2}+2x-2} \\[3ex] & \text{Example b.)} \hspace{2ex} y = \frac{x(3x^{2} \: - \: 2)}{5x^{3}+1} \hspace{2ex} \text{Becomes:} \hspace{2ex} y = \frac{3x^{3}-2x}{5x^{3}+1} \\[3ex] & \text{Example c.)} \hspace{2ex} y = \frac{x^{3} + 11}{(x+1)(x-1)} \hspace{2ex} \text{Becomes:} \hspace{2ex} y = \frac{x^{3} + 11}{x^{2} \: - \: 1}\end{align}$$

2. Determine the highest exponent x term of both the numerator and denominator and remove all other terms in both the numerator and denominator.

$$\begin{align} & \text{Example a.) From step 1:} \hspace{2ex} y = \frac{\boxed{2x^{2}}+6x}{\boxed{x^{3}}-x^{2}+2x-2} \hspace{2ex} \text{Becomes:} \hspace{2ex} y = \frac{2x^{2}}{x^{3}} \\[3ex] & \text{Example b.) From step 1:} \hspace{2ex} y = \frac{\boxed{3x^{3}}-2x}{\boxed{5x^{3}}+1} \hspace{2ex} \text{Becomes:} \hspace{2ex} y = \frac{3x^{3}}{5x^{3}} \\[3ex] & \text{Example c.) From step 1:} \hspace{2ex} y = \frac{\boxed{x^{3}} + 11}{\boxed{x^{2}} \: - \: 1} \hspace{2ex} \text{Becomes:} \hspace{2ex} y = \frac{x^{3}}{x^{2}}\end{align}$$

3. The function should now be a fraction that divides x raised to some power (the numerator's highest exponent x term) by x raised to some power (the denominator's highest exponent x term).

   Possibility #1 (Example a.)
   If the exponent in the numerator is lesser than the exponent in the denominator, there is a horizontal asymptote at y = 0.

   $$\begin{align} & \textbf{Example a.)} \\ & \text{From step 2:} \hspace{2ex} y = \frac{2x^{\boxed{2}}}{x^{\boxed{3}}} \hspace{1.5ex} \text{has a horizontal asymptote at } y = 0 \text{.} \end{align}$$

   Possibility #2 (Example b.)
   If the exponent in the numerator is equal to the exponent in the denominator, we divide the x out of the fraction and are left with a fraction of two constants, ^a⁄_b. The horizontal asymptote is located at y = ^a⁄_b.

   $$\begin{align} & \textbf{Example b.)} \\ & \text{From step 2:} \hspace{2ex} y = \frac{3x^{\boxed{3}}}{5x^{\boxed{3}}} \hspace{1.5ex} \text{has a horizontal asymptote at } y = \frac{3}{5} \text{.} \end{align}$$

   Possibility #3 (Example c.)
   If the exponent in the numerator is greater than the exponent in the denominator, there is no horizontal asymptote.

   $$\begin{align} & \textbf{Example c.)} \\ & \text{From step 2:} \hspace{2ex} y = \frac{x^{\boxed{3}}}{x^{\boxed{2}}} \hspace{1.5ex} \text{has no horizontal asymptote since } 3>2 \text{.} \end{align}$$

Finding the Horizontal Asymptotes of an Exponential Function

Some exponential functions take the form of y = b^x + c and therefore have a constant c. The horizontal asymptote of an exponential function with a constant c is located at y = c.

$$\begin{align} & \text{Example:} \hspace{1.5ex} y = 2^{x} + 5 \hspace{1.5ex} \text{has a constant } c = 5 \text{.} \\ \\ & \text{Therefore, it has a horizontal asymptote located at } y = 5 \text{.}\end{align}$$

Some exponential functions take the form of y = b^x and therefore do not have a constant c. The horizontal asymptote of an exponential function with no constant is located at y = 0.

$$\begin{align} & \text{Example:} \hspace{1.5ex} y = -3^{x} \hspace{1.5ex} \text{has no constant } c \text{.} \\ \\ & \text{Therefore, it has a horizontal asymptote located at } y = 0 \text{.}\end{align}$$