What is a Dot Product?

The dot product of two vectors sums the products of their corresponding components and returns a scalar. A scalar is a single number that does not have direction or components like a vector.

The dot product of two vectors is commonly notated as a∙b, where a and b are the vectors, and the dot operator "∙" represents that a dot product is being calculated. The two formulas used for calculating a dot product are given in the below sections Dot Product Calculation Method #1 and Dot Product Calculation Method #2.

Why do we Learn About the Dot Product?

The dot product is needed for solving many real-world science and engineering problems, so let's look at just one to see why it's such a valuable math operation: we can use the dot product to design a space rocket's trajectory into orbit for optimized fuel usage, launch cost, and payload capability.

Getting a rocket into orbit requires an immense amount of energy. We must lift a skyscraper-sized launch vehicle upwards to clear the dense air in Earth's lower atmosphere and then accelerate it to an extremely high horizontal speed (about 28,000 km/h, or 17,000 mph!) to achieve a stable orbit.

The image above is a long-exposure photograph of a SpaceX Falcon 9 rocket carrying a satellite into orbit. The shape of the rocket's trajectory is known as a gravity turn because it travels on a steep angle upwards, and then lets gravity pull its path over to the side and eventually to the horizontal.

The gravity turn's profile is carefully calculated prior to launch. This profile is then programmed into the rocket's guidance system and executed with precision during flight.

But how does the dot product tie into this? Well, the formula for work is given as:

$$\begin{align}& W = \vec{F} \cdot \vec{d} \\ \\ & \text{Where:} \\ & W \: \text{ is the work done} \\ & \vec{F} \: \text{ is the force vector} \\ & \vec{d} \: \text{ is the distance vector} \end{align}$$

The work-energy principle tells us that the work done on a system like a rocket is equal to its change in mechanical energy. So, the work done by the engines will be equal to the rocket's change in mechanical energy.

We can calculate the work done by a rocket's propulsion system by calculating the dot product of the various force and distance vectors throughout the ascent. By tweaking the gravity turn's profile, we can repeatedly compare the work done to the final state of the mechanical energy the rocket ends up in.

By knowing how to calculate the dot product of two vectors, we are able to optimize a rocket's launch profile for efficient fuel usage, minimal cost, and maximum performance!

Dot Product Calculation Method #1

The formula for dot product method #1 is given as:

$$\begin{align}& \vec{a} \cdot \vec{b} = (a_{1}b_{1}) + (a_{2}b_{2}) + (a_{3}b_{3}) \\ \\ & \text{Where:} \\ & \vec{a} = a_{1}i + a_{2}j + a_{3}k \: \text{ and } \: \vec{b} = b_{1}i + b_{2}j + b_{3}k \end{align}$$

Method #1 is very convenient to use because we perform three pure multiplication operations using the components from each vector, which are often provided in the problem. We then sum the multiplied terms to get the final dot product solution.

This method is not very convenient to use if we are given vector directions and magnitudes but not the i, j, and k components of the vectors. Method #2 may be easier to use for those kinds of problems. However, when we cannot determine the angle between vectors, we must use method #1.

Dot Product Calculation Method #2

The formula for dot product method #2 is given as:

$$\begin{align}& \vec{a} \cdot \vec{b} = \big| \vec{a} \big| \big| \vec{b} \big| cos( \theta ) \\ \\ & \text{Where:} \\ & \big| \vec{a} \big| \: \text{ is the magnitude of } \: \vec{a} \\ & \big| \vec{b} \big| \: \text{ is the magnitude of } \: \vec{b} \\ & \theta \: \text{ is the angle between } \: \vec{a} \: \text{ and } \: \vec{b} \end{align}$$

This method is great for use in 2-dimensional vector systems where the angle between the vectors is a known value and the Pythagorean theorem can be implemented to find the magnitude of each vector. Once the magnitudes and angle are known, just two multiplication operations need to be performed.

Additionally, this method can be used in a 3-dimensional vector system if we can determine the angle between the two vectors (or if given in the problem statement). If we are unable to determine the angle between the two vectors, we may consider using method #1 to calculate the dot product.

Example Problem

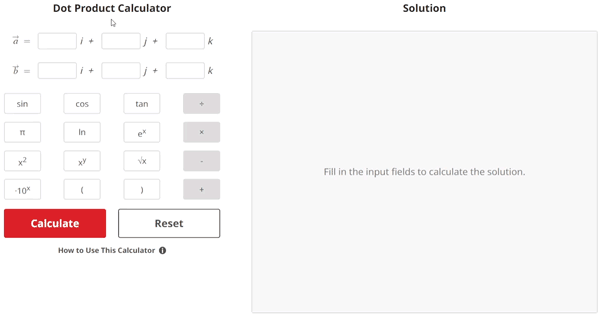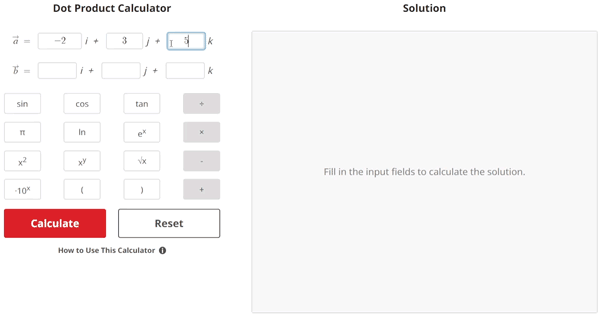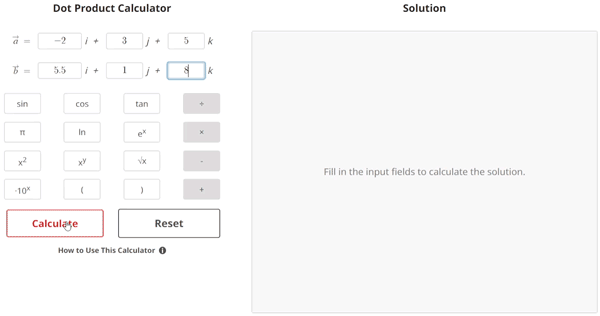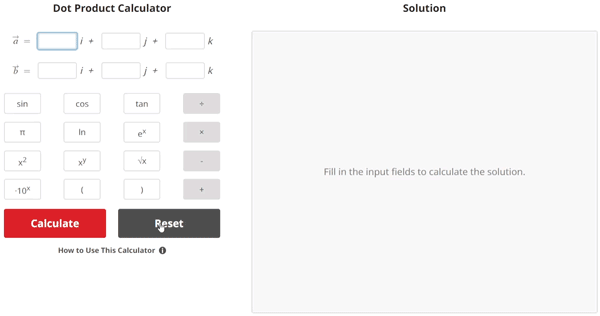
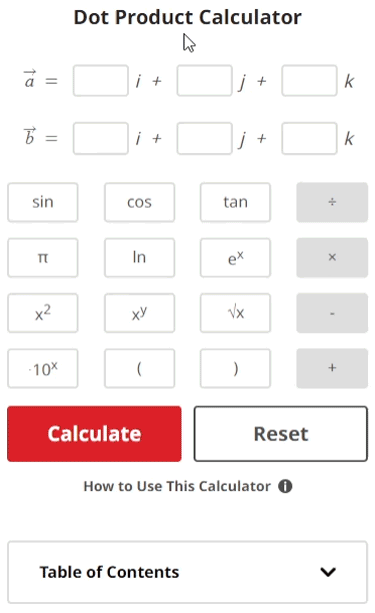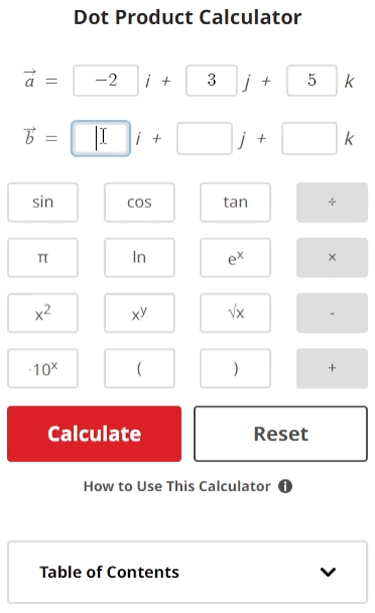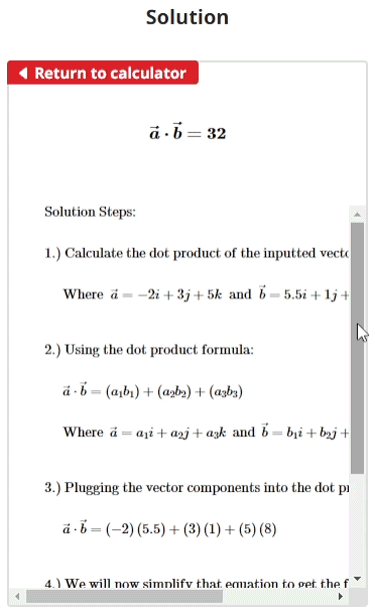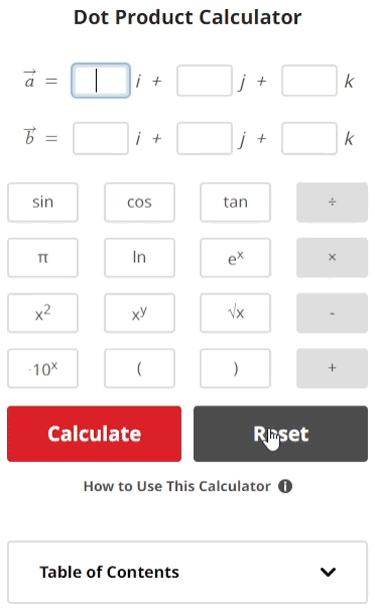
$$\begin{align}& \text{1.) Calculate the dot product of the two vectors } \: \vec{a} \: \text{ and } \vec{b} \\ \\ & \hspace{3ex} \text{Where } \; \vec{a} = -2i +3j +5k \; \text{ and } \; \vec{b} = 5.5i +1j +8k\\ \\ \\ & \text{2.) Using the dot product formula:} \\ \\ & \hspace{3ex} \vec{a} \cdot \vec{b} = (a_{1}b_{1}) + (a_{2}b_{2}) + (a_{3}b_{3}) \\ \\ & \hspace{3ex} \text{Where } \: \vec{a} = a_{1}i + a_{2}j + a_{3}k \: \text{ and } \: \vec{b} = b_{1}i + b_{2}j + b_{3}k\\ \\ \\ & \text{3.) Plugging the vector components into the dot product formula, we get:} \\ \\ & \hspace{3ex} \vec{a} \cdot \vec{b} = \left( -2\right) \left( 5.5\right) + \left( 3\right) \left( 1\right) + \left( 5\right) \left( 8\right) \\ \\ \\ & \text{4.) We will now simplify that equation to get the final value:} \\ \\ & \hspace{3ex} \vec{a} \cdot \vec{b} = \left( - 11\right) + \left( 3\right) + \left( 40\right) \\ \\ & \hspace{3ex} \vec{a} \cdot \vec{b} = - 11+ 3+ 40\\ \\ & \hspace{3ex} \vec{a} \cdot \vec{b} = \boxed{32}\end{align}$$

How the Calculator Works

The Voovers dot product calculator utilizes the programming languages HTML (HyperText Markup Language), CSS (Cascading Style Sheets), and JS (JavaScript). The HTML creates the skeleton of the calculator, the CSS adds visual styling to the skeleton, and the JS handles interactions with the interface, number crunching, and calculations.

The calculator's routine uses the same formula shown in dot product method #1 earlier in this lesson. It reads the user's inputted vector components, plugs them into the formula, and evaluates the equation until the single scalar answer is reached. In essence, the calculator solves for a dot product just as a person would!

Throughout the process of calculations, little snapshots of the progress during each step are taken. These snapshots are formatted into a math rendering programming language called LaTeX and displayed as the solution steps.