Algebra
Related Lessons
Tutors/teachers:
Nikkolas
Tutor and Aerospace Engineer
Discriminant
Lesson Contents
What is the Discriminant?
The discriminant is the part of the quadratic formula inside of the square root. For a quadratic ax2 + bx + c = 0, the discriminant is given as:
Discriminant = b2 – 4ac
The discriminant tells us how many roots a quadratic has. The relationship between result of discriminant and number of roots a quadratic has is given as:
b2 – 4ac > 0 — discriminant is positive — two real roots
b2 – 4ac = 0 — discriminant is zero — repeated real roots
b2 – 4ac < 0 — discriminant is negative — no real roots
The quadratic formula with the discriminant boxed in red.
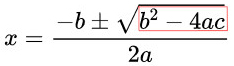
Why we use the Discriminant
The advantage of using the discriminant instead of just solving the full quadratic formula is that we get a quicker idea of how many roots the quadratic will have. Additionally, we get a quick and accurate idea of the type of roots.
For example, let’s look at a quadratic whose discriminant is zero. A discriminant of zero means there are repeated real roots. If we had graphed the quadratic, it may appear as only having a single root (location where the curve crosses the x-axis). Thanks to the discriminant, we know that there are actually repeated roots in the graph.
Example Problem
Use the discriminant to determine the number of and type of roots of the function f(x) = 3x2 + 4x + 1.
Solution:
1.) Since the function is a standard quadratic, let’s set a = 3, b = 4, and c = 1
2.) Plugging the constants into the discriminant, we get:
Discriminant = b2 – 4ac
Discriminant = (4)2 – 4(3)(1) = 16 – 12 = 4.
3.) The discriminant is 4, a positive number. Therefore, the given quadratic function has two real roots.
Result :
Worksheet 1
Download.pdf
Cheat sheet
Download.pdf