The Definition of an Arithmetic Sequence

An arithmetic sequence is a series of numbers where the difference between neighboring numbers is constant.

For example:

1, 3, 5, 7, 9, ...

Is an arithmetic sequence because 2 is added every time to get to the next term. The difference between neighboring terms is a constant value of 2.

Any ordered list of numbers is considered a sequence. A sequence that ends with "..." has an infinite number of terms. The "..." allows us to write the infinite sequence in shorthand to save time and space. The example sequence from above adds 2 to the previous number to get the next number, an infinite number of times.

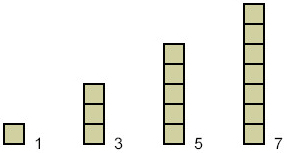
Sequences that are Arithmetic vs. Non-Arithmetic

There are sequences that progress to the next term by multiplying by a number, dividing by a number, or even adding or subtracting a number that changes with each successive term.

These are not arithmetic sequences. For a sequence to be arithmetic, the difference between a term and the next term must be constant. Please note that the difference between terms can be a positive or negative number. In other words, an arithmetic sequence can progress to larger numbers, or it can progress to smaller numbers.

Here's an example of a sequence that is arithmetic, and a sequence that is non-arithmetic:

• 1, 2, 3, 4, 5... (Adds 1 to each number, is arithmetic)
• 1, 3, 9, 27, 81... (Multiplies by 3, is non-arithmetic)

Real-World Uses of Arithmetic Sequences

Arithmetic sequences are found often in the real world. Sometimes they are leveraged by scientists and engineers to help solve problems. Other times, they are used to help count things that would otherwise be hard to sum up without the use of a sequence. Arithmetic sequences also naturally occur in nature.

Here's an example of an everyday use:

An auditorium has rows of seats that get wider as they progress from the stage to the back of the room. The first row has 10 seats, the row behind it has 2 more seats, and so forth. If the last row had 34 seats, this would be notated as a sequence as "10, 12, 14, 16, ..., 34". We can use the arithmetic sequence to easily determine how many seats are in the auditorium and therefore how many people can be seated at full capacity.

Examples of Arithmetic Sequences

• 21, 18, 15, 12, 9 ... (The difference is -3)
• -6, -10, -14, -18, -22 ... (The difference is -4)
• -2, -1, 0, 1, 2, 3, 4 ... (The difference is 1)
• 0, 12, 24, ..., 60. (The difference is 12 and the sequence ends at 60)
• 4, -1, -6, -11, ..., -36. (The difference is -5 and the sequence ends at -36)