How to Add and Subtract Scientific Notation

When numbers are expressed in scientific notation, we must match the powers of the base 10's before adding or subtracting them.

For example, 3.5 x 10⁴ and 6.1 x 10⁶ have different base 10 powers (the first number's base 10 is raised to the 4th power and the second number's base 10 is raised to the 6th power).

To add or subtract these numbers in scientific notation we will need to match the powers of the base 10's. We have three options for this, all of which will reach the same solution. We can:

1. Make the smaller power bigger to match the bigger power.
2. Make the bigger power smaller to match the smaller power.
3. Do a combination of #1 and #2 so the powers meet somewhere in the middle.

In this lesson we will show how to change scientific notation base 10 powers up or down. At the end of the lesson there are example problems for adding and subtracting in scientific notation.

How to Change the Power of the Base 10

Changing the power of the base 10 in scientific notation is simple. We can increase or decrease the power at will.

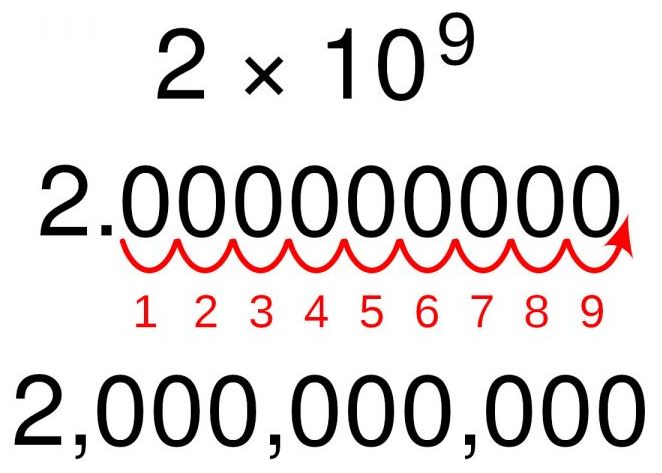
For every increase in the index of the power, we move the decimal to the left one place.

For example:
3.55 x 10⁴ = 0.0355 x 10⁶
We moved the base 10 power's index up by two and the decimal to the left by two places. Both scientific notation expressions equate to 35,500.

Likewise, for every decrease in the index of the power, we move the decimal to the right one place.

For example:
8.10 x 10⁵ = 8100.00 x 10²
We moved the base 10 power's index down by three and the decimal to the right by three places. Both scientific notation expressions equate to 810,000.

Example Problems

Let's go through a couple of example problems together to reinforce our ability to add and subtract scientific notation.

Adding Scientific Notation Example Problem

Find the sum of 2.50 x 10⁴ and 4.14 x 10³.

Solution:

1. Let's start by moving the second number's base 10 power up from 3 to 4 so we can then add the numbers.
2. 4.14 x 10³ = 0.414 x 10⁴
3. 2.50 x 10⁴ + 0.414 x 10⁴ = 2.914 x 10⁴

Subtracting Scientific Notation Example Problem

Find the difference 1.25 x 10⁷ - 5.00 x 10⁵.

Solution:

1. Let's try making the base 10 powers meet in the middle this time. We will do this by moving the first number's power down to 6 and second number's power up to 6.
2. 1.25 x 10⁷ = 12.50 x 10⁶
3. 5.00 x 10⁵ = 0.50 x 10⁶
4. 12.50 x 10⁶ - 0.50 x 10⁶ = 12.00 x 10⁶.
5. We currently have two digits left of the decimal. Let's reformat it to proper scientific notation format.
6. 12.00 x 10⁶ = 1.20 x 10⁷.